Giới thiệu về hình học Tôpô
Cùng với sự phát triển mạnh mẽ của các ngành khoa học tự nhiên, nhiều ngành toán học mới đã ra đời và phát triển như hình học Lobachevsky, Fractal, Tôpô (Topology)…Trong đó, hình học Tôpô xuất hiện chính thức từ giữa thế kỷ 19, là một trong các ngành toán học phức tạp và phát triển nhanh nhất của toán học hiện đại.
Tôpô bắt nguồn từ tiếng Hy Lạp là “Topologia” gồm topos (nghĩa là chỗ, vùng, miền…) và logos (nghĩa là nghiên cứu, tìm hiểu…). Đây là một ngành toán học nghiên cứu các đặc tính của đối tượng vẫn còn được bảo toàn qua các sự biến dạng như bẻ cong, kéo giãn, ép và xoắn nhưng ngoại trừ việc xé rách và việc dán dính.
Phép biến đổi Tôpô không bảo toàn tỉ lệ, các yếu tố đo lường (kích thước, độ dài, diện tích, thể tích, góc…) và các hướng mà chỉ bảo tồn tính liên tục và mối quan hệ lân cận của bề mặt. Có thể nói, hình học Tôpô quan tâm tới phân tích định tính chứ không phải là định lượng. Những thuộc tính được duy trì sau các biến dạng như vặn, xoắn, kéo giãn… được gọi là các bất biến tôpô. Một hình dạng hình học, dưới các tác động của sự biến dạng, khiến chúng có thể mất đi mọi thuộc tính về hình dạng và kích thước mà vẫn duy trì được tính chất định tính của nó – Thì hình trước và sau khi biến đổi gọi là tương đương tôpô.
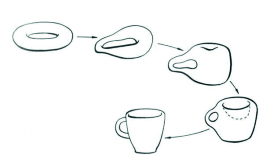
Ví dụ, dưới quan điểm của tôpô học, chúng ta không thể phân biệt được một cái bánh vòng và một cái cốc có quai vì cả hai đều là vật rắn và đều có duy nhất một lỗ hổng (hình 1). Hãy hình dung vẽ một hình tròn lên tấm cao su, sau đó bằng cách kéo giãn, bóp nén, bẻ cong, xoắn nhưng không nhập hay chồng lấp thì nó có thể biến dạng thành một hình vuông, elip, tam giác… loại trừ hình số 8 vì không thể kéo giãn hình tròn thành hình số 8 mà không đục xé nó thêm một lỗ. Như vậy, hình tròn tương đương tôpô với hình vuông, elip, tam giác… nhưng hoàn toàn phân biệt với hình số 8. Đây cũng là lý do người ta mệnh danh Tôpô là “hình học màng cao su”. Từ đó, có thể nói rằng Tôpô là khoa học của biến dạng và cũng là khoa học của bất biến.
Lý thuyết không gian hình học Tôpô và khả năng sáng tạo kiến trúc
Việc hình học Tôpô ra đời và phát triển đã ảnh hưởng sâu sắc đến cả văn học, nghệ thuật, triết học và sau đó là kiến trúc. Dù tiếp cận Tôpô muộn hơn các ngành nghệ thuật khác nhưng các KTS đã nhanh chóng bị hấp dẫn và tìm được nguồn cảm hứng mạnh mẽ để sáng tạo nên những không gian mang tính siêu thực, độc đáo và vô cùng mới mẻ.
Nhắc đến hình học Tôpô, người ta thường nói đến khái niệm: Mạng lưới, nút, dải Moebius và chai Klein…Đây cũng là những cơ sở khơi gợi tư duy sáng tạo mới, quan điểm mới về hình khối và không gian trong kiến trúc.
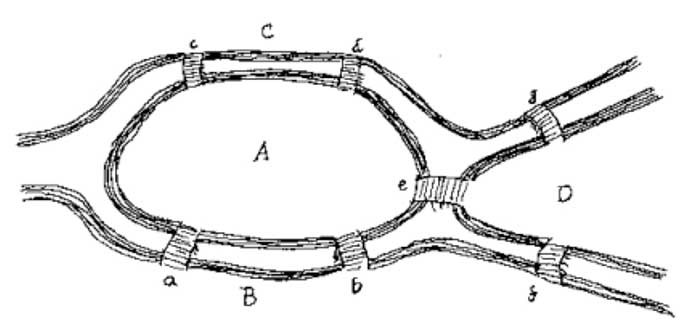
– Mạng lưới: Hình học Tôpô nghiên cứu sự liên tục của không gian bằng các mạng lưới, từ năm 1735, nền móng của Tôpô học đã được nhà toán học Euler đưa ra với bài toán “Bảy cây cầu ở Königsberg”. Thành phố Königsberg, Đức (nay là Kaliningrad, Nga) nằm trên sông Pregel, bao gồm hai hòn đảo lớn nối với nhau và với đất liền bởi bảy cây cầu (hình 2). Bài toán đặt ra là tìm một tuyến đường mà đi qua mỗi cây cầu một lần và chỉ đúng một lần (bất kể điểm xuất phát hay điểm tới).
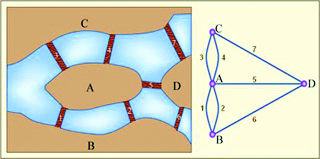
Để tìm câu trả lời cho bài toán, Euler đã rút ra rằng thông tin quan trọng là số cây cầu và danh sách các vùng đất ở đầu cầu thay vì diện tích các vùng đất hay vị trí chính xác của chúng. Từ đó, ông đã loại bỏ tất cả các chi tiết không cần thiết (ngoại trừ các vùng đất và các cây cầu), sau đó thay thế mỗi vùng đất bằng một điểm gọi là đỉnh hoặc nút, mỗi cây cầu bằng một đoạn nối gọi là cạnh hoặc liên kết. Cấu trúc toán học thu được gọi là một đồ thị. Hình thù của đồ thị có thể bị bóp méo, biến dạng theo nhiều cách nhưng không làm cho đồ thị thay đổi, miễn là các liên kết giữa các nút được giữ nguyên theo hình 2, đồ thị có một nút bậc 5 và 3 nút bậc 3. Euler đã chứng minh tuyến đường mà bài toán đặt ra chỉ có thể tồn tại khi và chỉ khi đồ thị không có nút bậc lẻ. Do đồ thị bảy cây cầu ở Königsberg có 4 nút bậc lẻ nên câu trả lời của bài toán là không thể.
Đây là biểu đồ đầu tiên và là sự xuất hiện đầu tiên của hình học Tôpô. Vấn đề đã được thu gọn lại về bản chất của nó. Cấu trúc hình học được biến đổi thành một cấu trúc linh hoạt mà không quan tâm đến hình thù cứng nhắc của các đối tượng, một đặc điểm của hình học Tôpô sau này. Đây cũng là tiền đề có ảnh hưởng lớn đến lý thuyết đồ thị, lý thuyết mạng lưới được sử dụng trong các lĩnh vực rộng lớn như sinh học, sinh thái học, khoa học xã hội, kinh tế, tài chính, cơ sở hạ tầng đô thị, an ninh quốc gia.
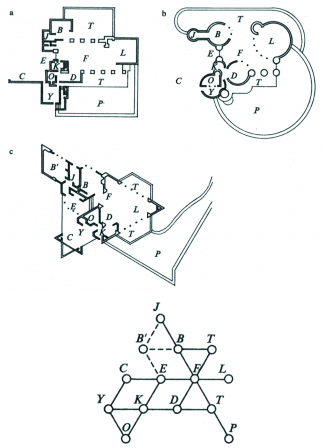
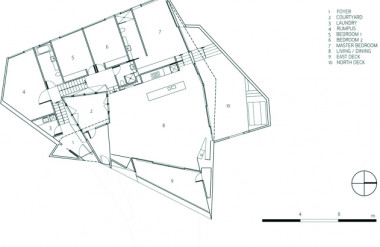
Thuyết đồ thị cũng đã được áp dụng nhiều trong quá trình thiết kế kiến trúc. Lý thuyết này giúp các KTS phân tích các hoạt động chức năng của công trình. Hãy quan sát mặt bằng ba ngôi nhà được thiết kế bởi KTS lỗi lạc Frank Lloyd Wright (hình 3). Hai ngôi nhà a và b đều được thiết kế vào năm 1938 và ngôi nhà còn lại được thiết kế 2 năm sau đó. Ba thiết kế này hoàn toàn khác nhau với các mặt bằng lần lượt vuông vức, cong tròn mềm mại và đa giác. Tuy nhiên, sơ đồ liên kết không gian giữa các phòng thì không thay đổi (chỉ có Sundt House là có thêm phòng ngủ – tương ứng nút B’ trên sơ đồ liên kết). Qua sơ đồ liên kết dễ dàng thấy được thực sự cả ba mặt bằng này đều tương đương hình học Tôpô với nhau.
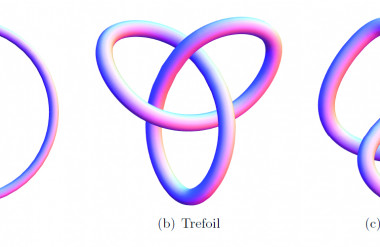
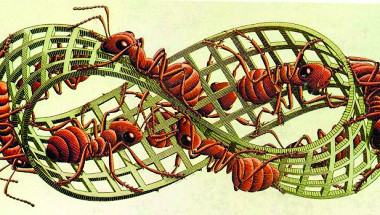
– Nút: Một nút trong không gian ba chiều đơn giản là một vòng tròn thắt nút. Lấy một sợi dây, quấn một cách tùy ý rồi nối hai đầu sợi dây lại với nhau ta được một nút. Nút là một vật thể cơ bản của không gian. Có thể nói, nút đơn giản chỉ là một đường cong khép kín trong không gian (hình 4, 5).
Khả năng nghiên cứu nút trong ngành toán học được Carl Frederic Gauss phát hiện vào đầu thế kỉ 19, sang thế kỷ 20, lý thuyết nút phát triển mạnh như một bộ phận của Tôpô hình học nhờ những tiến bộ lớn trong ngành này. Gần đây đã bắt đầu xuất hiện những khả năng ứng dụng lý thuyết nút trong vật lý, hoá học và sinh học (chẳng hạn trong nghiên cứu DNA).
Chủ đề nút đã cuốn hút một cách mạnh mẽ trong nhiều lĩnh vực của văn học, nghệ thuật và khoa học, như Jean-Michel Kantor đã viết: “Chủ đề nút đã gây cảm hứng lớn lao cho nhiều lĩnh vực văn học, nghệ thuật, dân tộc học, và khoa học trước khi trở thành đối tượng của một lý thuyết toán học tiên tiến. Các nút đúng là một cách đơn giản để thoát khỏi sự trì độn của không gian: Sự hiện diện của các nút lật đổ môi trường của chính nó. Từ mê cung của Leonardo tới chiếu sáng thời trung cổ, và từ các trò chơi Eskimo đến các kỹ thuật đánh bắt cá, các chủ đề của nút đang lan rộng khắp tất cả các nền văn hóa trên thế giới. Và đây là một ví dụ cơ bản của topology: Các biến dạng của chuỗi chính xác là các biến dạng được ủy quyền cho các nhà tôpô học”.
Jean-Michel Kantor cũng ví toán học như một kho tàng Ali Baba khổng lồ chứa đầy châu báu mà hàng thế kỷ qua, các nền văn hóa khác nhau trên thế giới, các du khách đã tìm đến để tìm kiếm những khái niệm, ý tưởng, hình thức và kết quả. Các KTS cũng không ngoại lệ, luôn tìm được nguồn tài nguyên hữu ích ở đó. Và hình học Tôpô chính là một ngách quan trọng và lý thú trong cái hang kỳ bí ấy. Các nút, không chỉ là vật liệu dệt nên thơ ca hay các bức họa mà còn là nguyên liệu cho các ý tưởng kiến trúc độc đáo. Từ năm 2001-2006, UN studio đã thiết kế dự án bảo tàng Mercedes-Benz lấy cảm hứng từ một nút chẽ ba (hình 6).
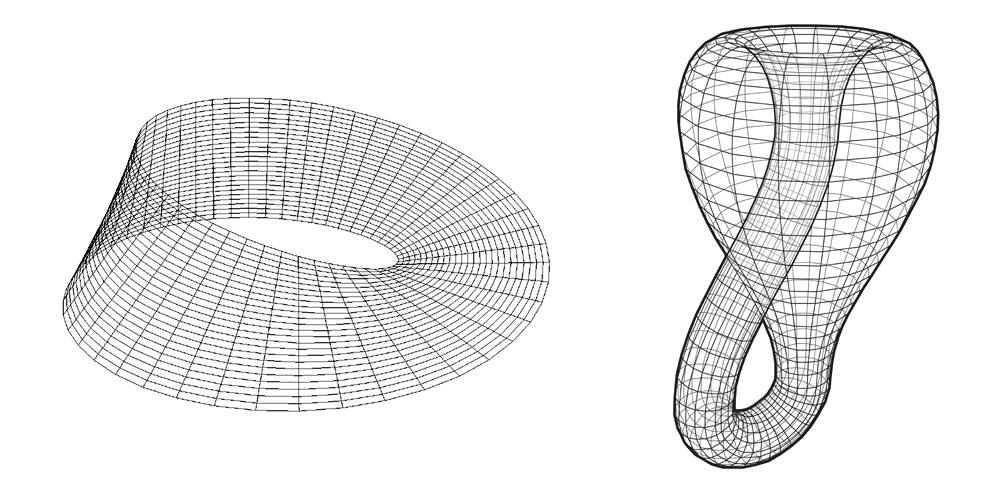
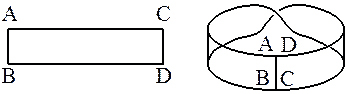
– Dải Moebius và chai Klein: Dải Moebius được nhà toán học và nhà thiên văn học August Ferdinand Moebius mô tả lần đầu tiên vào năm 1858 tại Paris như là một bề mặt mới trong không gian ba chiều. Để tạo ra dải Moebius, ta cần một băng giấy hình chữ nhật đủ dài. Gọi A, B, C, D là 4 đỉnh của hình chữ nhật đó. Giữ một đầu dải của hình chữ nhật bằng một tay (ví dụ giữ đầu AB). Xoay đầu CD một góc 1800 dọc theo trục ngang của giải sao cho A gặp D và B gặp C (hình 7). Như vậy việc xây dựng dải Moebius đã hoàn tất.
Với một động tác đơn giản, bề mặt đã bị biến dạng mà không có vết cắt hay xé, vòng quay thực hiện trên một đầu của dải đã biến đổi sâu sắc tính chất của nó. Nếu một con kiến bò dọc theo chiều ngang của dải, nó sẽ quay trở lại chính nơi nó bắt đầu mà không cần phải vượt qua các cạnh của dải (xem hình 8), như vậy có thể nói dải Moebius chỉ có một mặt. Tương tự, nếu ta chạy dọc ngón tay trên cạnh biên của dải thì ngón tay của ta sẽ quay trở lại chính điểm xuất phát, do đó dải Moebius cũng chỉ có một cạnh (hay một đường bao). Từ các ví dụ nêu trên có thể nói Moebius là bề mặt mà trên đó không thể xác định được phương hướng.
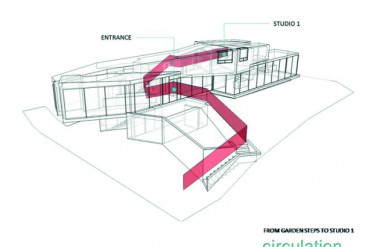
Tính chất liên tục, vô hướng, vặn xoắn và linh động của dải Moebius đã giúp cho các KTS thỏa sức sáng tạo nghệ thuật. Hai ví dụ điển hình là ngôi nhà Moebius của Van Berkel và tòa nhà Max Reinhardt tại Đức do Peiter Einsenman thiết kế (hình 9). Ngôi nhà Moebius đã được KTS Ben Van Berkel áp dụng tư duy hình học Tôpô vào thiết kế kiến trúc, lấy ý tưởng từ dải Moebiusđược chính tác giả nói về công trình của mình như sau: “Các mô hình toán học của dải Moebius không được chuyển tải theo nghĩa đen cho tòa nhà, nhưng khái niệm hoặc tư tưởng của nó có thể được tìm thấy trong các thành phần kiến trúc, chẳng hạn như ánh sáng, cầu thang và cách thức mà con người di chuyển qua ngôi nhà”.
Dải Moebius đã không được áp dụng một cách nghiêm ngặt về mặt toán học vào công trình, bởi những đối tượng của hình học Tôpô là trừu tượng và không thể hình dung một cách chính xác bằng các mô hình.Tuy nhiên, các đặc điểm, tính chất đặc trưng về không gian và thời gian của nó đã được KTS lĩnh hội, chắt lọc và truyền tải vào công trình kiến trúc. Đây cũng chính là cách các KTS tìm tòi, khám phá và tiếp nhận những tinh hoa của hình học Tôpô trong cái hang Ali Baba huyền diệu chứa đầy các chất liệu ma thuật của toán học.
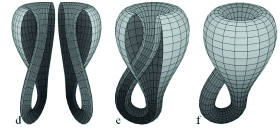
Ghép hai dải Moebius lại với nhau ta sẽ có một chai Klein (hình10). Giống như dải Moebius, chai Klein là một cấu trúc hình học không thể định hướng mà giao cắt với chính nó. Có thể nói, chai Klein là một tương ứng ba chiều của dải Moebius. Sự giao thoa phức tạp giữa bên trong và bên ngoài của chai Klein đã khơi gợi ý tưởng cho KTS McBride Charles Ryan thiết kế ngôi nhà Klein bottle ở Mornington Peninsula, VIC, Australia. Tác giả đã cố gắng gửi gắm tư tưởng của chai Klein trong không gian kiến trúc phức tạp của ngôi nhà (hình 11).
(Còn tiếp Phần 2)
Tài liệu tham khảo:
1. Cornelie Leopold: Visual methodologies for designing, 2012
2. Cornelie Leopold: Geometry concepts in Architectural design, 2006
3.Cornelie Leopold: Architecture and geometrical space conceptions, 2002
4. Prof. Michele Emmer : Mathland, From Topology to Virtual Architecture, 2004
5. Zaihui Li, Qinghua Chang, and Yuan Shen: Influence and Application of Topological Geometry in Architectural Design, 2012
6. Jean Michel Kantor: A Tale of Bridges: Topology and Architecture, 2005
7. Tô Bảo Thanh: Kiến trúc tham số, Luận văn thạc sĩ, trường đại học Kiến trúc Tp. Hồ Chí Minh, 2012
8. Đoàn như Kim: Một số khái niệm về hình học trong kiến trúc, 2005
9. Nguồn internet: https://vi.wikipedia.org; http://www.math.hcmuns.edu.vn; http://blog.kleinproject.org; http://www.archdaily.com; http://designs.vn…
10. Jean-Michel
11. Kantor
KTS. Nguyễn Thị Minh Thùy
(Bài đăng trên Tạp chí Kiến trúc số 4 – 2017)