Nghiên cứu sự phát triển cấu trúc hình học trong tạo hình kiến trúc

Tóm tắt

Có thể nói, hình học là một trong những đại diện cho nền tảng tư duy và văn minh của xã hội loài người. Đối với kiến trúc, hình học là nền tảng cơ bản cho tạo hình thiết kế. Hình học “là nguyên tắc tổ chức, là phương tiện nối các bộ phận của kiến trúc lại với nhau” [1]. Ngoài hình học Euclid truyền thống được nhiều người biết đến, các loại hình học khác cũng đã được hình thành, kéo theo sự xuất hiện của rất nhiều khái niệm hay cấu trúc hình học mới. Cùng với sự phát triển của đồ họa và công nghệ xây dựng, việc ứng dụng các cấu trúc hình học trong thiết kế, xây dựng thực tiễn ngày càng trở nên đa dạng với nhiều cấp độ phức tạp hơn. Bài báo này tổng hợp, hệ thống và khái quát một số đặc điểm chính về sự phát triển của cấu trúc hình học trong tạo hình kiến trúc theo các giai đoạn phát triển khoa học của nhân loại.

Từ khóa: Hình học kiến trúc, cấu trúc hình học, tạo hình kiến trúc.

1. Một số khái niệm

• Cấu trúc hình học: Đó là một tạo hình từ đơn giản đến phức tạp, có thể được tạo ra từ một (dạng đơn thể) hoặc nhiều (dạng tổ hợp) yếu tố hình học cơ bản (còn gọi là các khái niệm hình học cơ bản hay hình thể không gian) đã được định nghĩa thuộc các dạng hình học khác nhau.
• Tạo hình kiến trúc: Trong phạm vi nghiên cứu, tạo hình kiến trúc là hình dáng tổng thể của công trình kiến trúc hay còn gọi là hình thể kiến trúc [2], là một cấu trúc hình học tạo nên từ một hoặc là tổ hợp nhiều hình thể không gian liên kết nhau, có kích thước hay quy mô dựa trên công năng, nhu cầu sử dụng và ý đồ nhà thiết kế. Ví dụ: Tòa nhà Quốc hội Brazil do KTS Oscar Niemeyer thiết kế có tạo hình kiến trúc dạng tổ hợp từ các khối hộp chữ nhật và bán cầu liên kết nhau.

• Thiết kế tạo hình kiến trúc: Là một phần quan trọng của sáng tác kiến trúc hay thiết kế tổ hợp kiến trúc, như Gaudet đã định nghĩa, đó là: “Sự kết hợp của các bộ phận trong một tổng thể thống nhất” [4]. Cụ thể hơn, thiết kế tạo hình kiến trúc là việc tổ chức, bố cục, sắp xếp hình thể không gian của các thành phần trong công trình để có được sự thống nhất ngay từ bên trong (nội thất) ra đến hình khối mặt đứng bên ngoài (ngoại thất), tạo ra hiệu quả thẩm mỹ đặc thù, phù hợp về công năng của kiến trúc [4, 5, 6,7].

Trong giới hạn nghiên cứu của bài báo, khái niệm cấu trúc hình học được nghiên cứu là tạo hình tổng thể hay hình khối tổng thể của công trình, không đi sâu vào các chi tiết trang trí nhỏ.

2. Cấu trúc hình học trong tạo hình kiến trúc giai đoạn trước cách mạng công nghiệp (thế kỷ 18)

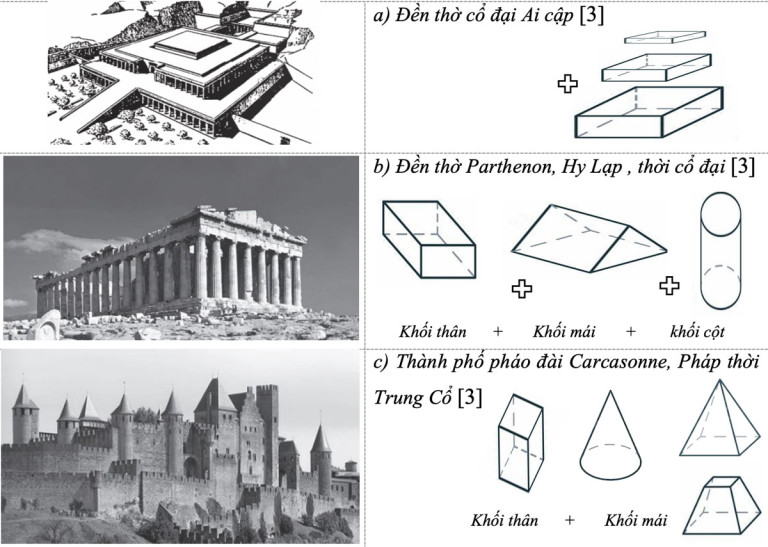
Giai đoạn này, hình học Euclid đóng vai trò chủ đạo. Do những hạn chế về khoa học, công nghệ xây dựng và vật liệu (gạch, gỗ, đá, …) kiến trúc trước cách mạng công nghiệp thường có tạo hình từ các khái niệm cơ bản thuộc hình học Euclid là: Hình kỷ hà, đa diện, cầu, nón tròn xoay,… Ví dụ, kim tự tháp Ai cập có tạo hình từ các khối đa diện dạng chóp đáy hình vuông, đấu trường La Mã tạo hình từ khối trụ tròn xoay,…

Các công trình kiến trúc giai đoạn cổ và trung đại thường là sự phối hợp đơn giản theo các nguyên tắc cộng trừ khối các cấu trúc căn bản dạng đơn thể thuộc hình học Euclid mà không dùng có quá nhiều biến thể hình học. Ví dụ: Đền thờ cổ Ai cập là phép lặp, chồng tầng đơn giản của các khối hộp có tỷ lệ nhỏ dần; Đền thờ Parthenon, Hy Lạp là sự cộng trừ các khối đa diện dạng trụ chữ nhật, tam giác và các thức cột dạng trụ tròn xoay; Thành phố pháo đài Carcasonne, Pháp thời Trung Cổ là một tổ hợp hình khối cơ bản, trong đó thân công trình là các khối trụ tròn hoặc chữ nhật, mái từ các khối chóp, chóp cụt hoặc nó tròn xoay…

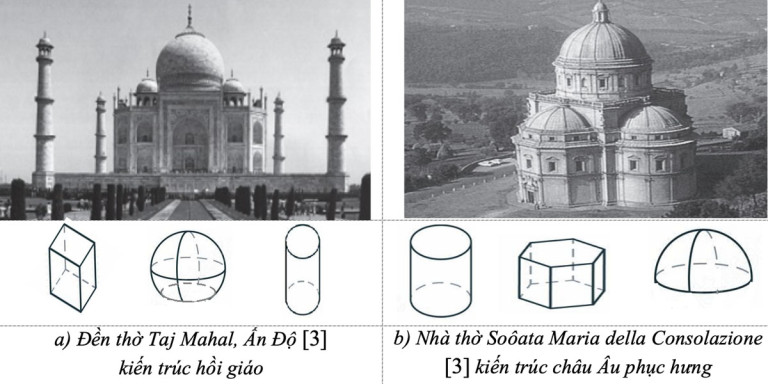
Sự khác biệt về phong cách kiến trúc trong giai đoạn này được thể hiện thông qua đặc điểm tạo hình kiến trúc gắn với việc lặp lại một số cấu trúc hình học có hình dáng, tỉ lệ và theo những cách nhất định. Ví dụ: Kiến trúc đền thờ Hồi giáo thường hay vận dụng cấu trúc dạng cầu làm mái, đặt trên thân công trình dạng trụ hộp chữ nhật đứng, trong khi đó kiến trúc đền thờ hoặc lâu đài châu Âu thì thường có mái là cấu trúc dạng chóp (nón tròn xoay, chóp tứ giác) hoặc nếu mái dạng cầu thì là dạng bán cầu đặt trên thân công trình hình trụ tròn xoay hoặc lăng trụ đều.

3. Cấu trúc hình học trong tạo hình kiến trúc giai đoạn sau cách mạng công nghiệp (sau thế kỷ 18)

Giai đoạn này đánh dấu sự phát triển mới của văn minh nhân loại, trong đó có hình học. Các loại hình học phi Euclid ra đời, kéo theo sự xuất hiện của các cấu trúc hình học mới như Eliptic, Hyperboloid, Mặt cong kẻ như Hypecbolic paraboloid,… Thông thường, việc ra đời của các cấu trúc hình học mới chưa tác động ngay tới tạo hình kiến trúc xây dựng mà thường một thời gian sau (vài thập kỷ hoặc đôi khi là cả thế kỷ), khi công nghệ vật liệu và kết cấu phát triển đến độ nhất định, các cấu trúc hình học ra đời sau Euclid mới có thể được ứng dụng. Các trường phái kiến trúc hiện đại, hậu hiện đại, hiện đại mới hình thành và phát triển mạnh mẽ từ sau chiến tranh thế giới thứ hai. Một số xu thế chính sử dụng cấu trúc hình học trong các trào lưu kiến trúc sau cách mạng công nghiệp và chiến tranh thế giới thứ 2 có thể khái quát như sau:

Xu thế thứ nhất: Tiếp tục sử dụng hình học Euclid làm chủ đạo, tạo hình theo hướng lược giản các chi tiết trang trí đắp bằng vữa hay xi măng, nhấn mạnh hơn với các khối lớn, thể hiện vẻ đẹp của kết cấu và các vật liệu mới sau cách mạng công nghiệp như sắt, kính, bê tông.

Ví dụ Bảo tàng Gugenhein do KTS Frank Loy Wright thiết kế 1959, một trong những công trình kiến trúc hiện đại nổi tiếng là sự tổ hợp của nhiều khối hình học cơ bản, phô diễn vẻ đẹp khỏe khoắn của chất liệu bê tông.

Xu thế thứ hai: Thay vì chỉ dùng các cấu trúc nguyên thể, các kiến trúc hiện đại, hiện đại mới đã sử dụng những tạo hình cắt ghép từ các khối hình học cơ bản, tạo ra hình cấu trúc phức tạp và độc đáo hơn. Ví dụ, công trình Nhà hát Sydney Opera house (1973) là tổ hợp được cắt ghép từ các mảnh của khối cầu.

Xu thế thứ ba: Cấu trúc hình học phi Euclid bắt đầu đươc áp dụng nhờ những tiến bộ của công nghệ xây dựng, tạo ra những đột phá về hình thức so với giai đoạn trước. Tháp nước Shukhov thiết kế năm 1986 bởi KTS, kỹ sư xây dựng người Nga Vladimir Shukhov – Đây là công trình đầu tiên ứng dụng cấu trúc hình học Hyperboloid, một trong những cấu trúc hình học phi Euclid.

Đó cũng là sự mở đầu cho trào lưu ứng dụng các cấu trúc mới trong kiến trúc hiện đại sau này.

Ví dụ: Nhà thờ Roncham do KTS Le Corbusier thiết kế năm 1955 có tạo hình là mảnh cắt ghép từ cấu trúc Hyperbolic Paraboloid (Hình 08a); Nhà hàng Los Manantiales ở Xochimilco, Thành phố Mexico (1958) được thiết kế bởi KTS, kỹ sư xây dựng Felix Candela, người đi đầu trong viêc phát triển cấu trúc Hyperbolic Parabolid cho kết cấu bê tông vỏ mỏng; Sân vận động Olympic Tokyo của KTS Kenzo Tange (năm 1964) được thiết kế với cấu trúc hình học từ mặt cong dạng kẻ.

3. Giai đoạn từ cách mạng khoa học công nghệ (từ những năm 1970 đến nay)

Giai đoạn cách mạng công nghệ này đánh dấu sự phát triển vượt bậc của đồ họa máy tính dẫn tới khái niệm kiến trúc tham số và sự ra đời của hình học Fractal.

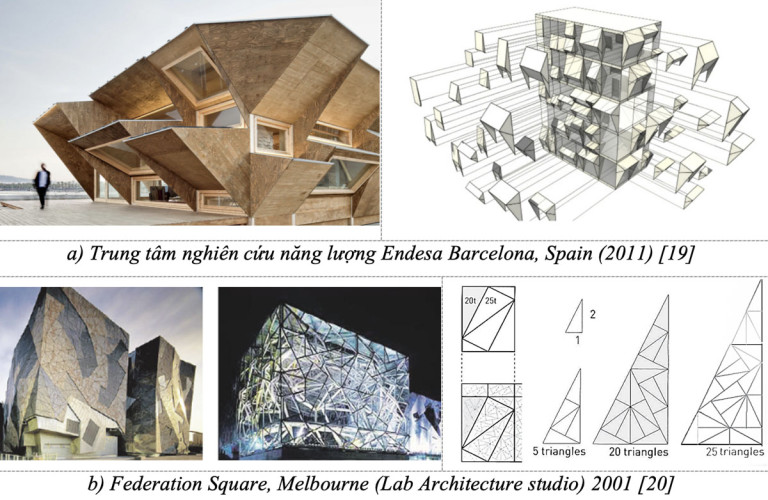
Hình học Fractal: Là phân nhánh toán học chuyên nghiên cứu đối tượng là các tổ hợp hình học Fractal (đặc điểm, cách tạo hình,…). Đó là khái niệm trừu tượng dùng để mô tả các sự vật tổ hợp từ nhiều phần nhỏ, hình thành một cách tự nhiên, có hình dạng gấp khúc trên mọi tỷ lệ phóng đại. Trong đó, mỗi phần nhỏ hơn lại tương tự hoặc giống như tổng thể hoặc phân đoạn lớn hơn chứa phần đó. Như vậy, mỗi tổ hợp hình học Fractal “có vô tận các chi tiết, các chi tiết này có thể có cấu trúc tự đồng dạng ở các tỷ lệ phóng đại khác nhau. Nhiều trường hợp, có thể tạo ra tổ hợp Fractal bằng việc lặp lại một mẫu toán học, theo phép hồi quy [14, 15, 16]. Ví dụ đơn giản của một tổ hợp hình học Fractal có trong tự nhiên (Hình 09) là cành cây nhiều nhánh, và mỗi nhánh lại có nhiều cành khác nhỏ hơn. Nếu cắt một cành ra thì sẽ thấy nó rất giống với toàn bộ thân cây hoặc nhánh cây lớn hơn chứa nó. Quan sát lá cây dương xỉ, ta cũng sẽ thấy mỗi nhánh lá là một hình ảnh của cả một cành lá và chi tiết hơn nữa cũng vậy.

Dưới sự ảnh hưởng của hình học Fractal, nhiều kiến trúc có bề mặt che phủ có họa tiết phức tạp hoặc cấu trúc dạng tổ hợp từ nhiều chi tiết tương tự, đồng dạng đã xuất hiện góp phần tạo nên một trào lưu kiến trúc mới – kiến trúc Fractal. Sự phát triển của công nghệ đồ họa giúp việc ứng dụng các tạo hình dạng Fractal phức tạp ngày càng trở nên khả thi hơn. Hình 10 là ví dụ một số công trình kiến trúc đương đại ứng dụng cấu trúc tự đồng dạng Fractal cho tạo hình thiết kế: Trung tâm nghiên cứu năng lượng Endesa Barcelona, Spain (2011) vận dụng các tạo hình đồng dạng lăng trụ tam giác cho hình khối và công trình trung tâm quảng trường Liên Bang, Melbourne (2001) ứng dụng cấu trúc tam giác Sierpinski trong hình học Fractal làm sơ đồ lưới thép không gian cho hệ vỏ bao che.

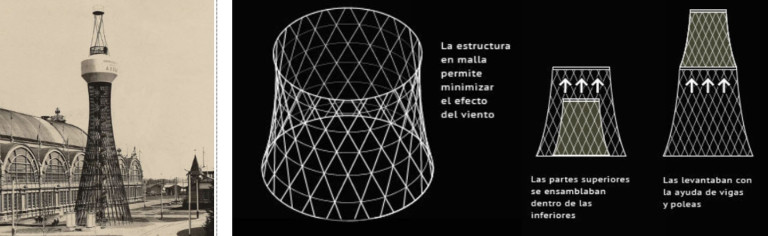
Từ sau cách mạng công nghệ, khái niệm kiến trúc tham số hình thành như là kết quả của việc ứng dụng đồ họa trong sáng tác kiến trúc. Cùng với sự hỗ trợ của máy tính, bên cạnh cấu trúc hình học Fractal, các cấu trúc tự do rất phát triển: Cấu trúc dạng lưới, dạng Nurbs (Non-Uniform Rational B-Splines)… đưa đến các tạo hình kiến trúc mới như tạo hình dạng nước (blob geometry); dạng nếp gấp (Folded geometry), dạng vô định hình (formless geometry) [10] (tham khảo hình 11). Trong giai đoạn này, “tính lưu động” (Fluidity) của cấu trúc tự do được nâng tầm bởi các KTS hàng đầu thế giới như Zaha Hadid, góp phần tạo thành một xu thế đương đại mới (Fluid architecture [21]).

Hình 12: Một số kiến trúc đương đại với tạo hình lưu động ứng dụng cấu trúc mặt cong tự do

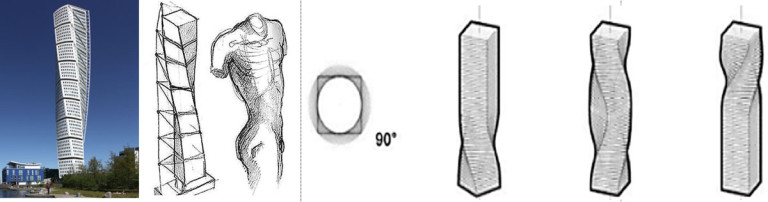
Ngoài hình dạng Fractal hay dạng cong tự do, từ sau cách mạng công nghệ, các khái niệm hay cấu trúc hình học đã có từ giai đoạn trước đó vẫn tiếp tục được sử dụng nhưng có sự biến đổi độc đáo hơn thông qua các biến đổi dạng topo (bóp méo, vặn, xoắn). Ví dụ: Tòa nhà tháp Turning Torso do KTS Calatrava thiết kế tại Thụy Điển (2005) được biến đổi theo hướng vặn xoắn khối trụ chữ nhật.

Với những tiến bộ về vật liệu, kết cấu, các kiến trúc hiện đại ứng dụng các cấu trúc phi Euclid từ giai đoạn trước đó cũng tạo ra những hình thức khác biệt, độc đáo hơn. Ví dụ: Nếu trong giai đoạn sau chiến tranh thế giới thứ 2, mặt Hyperbolic parboloid phát triển dựa trên vật liệu bê tông vỏ mỏng thì trong nhưng năm gần đây, cấu trúc này được áp dụng nhiều với vật liệu tre,… Hình 13 là một số ví dụ về cấu trúc phi Euclid áp dụng cho một số kiến trúc đương đại.

Ngày nay, các trào lưu kiến trúc đương đại như: Kiến trúc tham số, kiến trúc giải tỏa kết cấu, kiến trúc hữu cơ, kiến trúc phỏng sinh học,… đều đi liền với nhiều hình thức phong phú. Vì thế, kiến trúc hiện đại có thể kết hợp sử dụng nhiều dạng cấu trúc hình học khác nhau, tạo ra các màu sắc kiến trúc đa dạng.

4. Kết luận

Cấu trúc hình học là một phần tất yếu của tạo hình kiến trúc. Hình học Euclid với các cấu trúc căn bản như trụ, cầu, hộp, đa diện,… là nền tảng cho các thiết kế nói chung. Tuy vậy, cùng với sự phát triển của khoa học kỹ thuật, nhiều loại hình học phi Euclid đã lần lượt ra đời, có mối quan hệ chặt chẽ và là động lực cho sự ra đời của các trào lưu kiến trúc mới mà tạo hình ngày càng phức tạp và độc đáo. Việc nghiên cứu và sáng tác tạo hình theo các trào lưu kiến trúc đương đại đòi hỏi các nhà thiết kế phải có các hiểu biết sâu sắc về hình học và đồ họa. Tuy vậy, hiện nay, ở Việt Nam, các nghiên cứu về cấu trúc hình học, đặc biệt là các cấu trúc hình học hiện đại chưa nhiều. Phần lớn các nghiên cứu đã có hoặc thiên về thủ pháp nghệ thuật tạo hình, hoặc thiên về mô tả các khái niệm hình học riêng lẻ và đều chưa cập nhật đầy đủ cấu trúc hình học hiện đại mới ví dụ như hình học Fractal, hình học Topo,… Chính vì thế, rất cần các nghiên cứu chuyên sâu về cấu trúc hình học để góp phần thúc đẩy sự hội nhập về khoa học công nghệ của kiến trúc Việt Nam và thế giới.

TS.KTS. Lê Thị Phương Chi
Khoa Kiến trúc và Quy hoạch, Trường ĐH Xây dựng Hà Nội
(Bài đăng trên Tạp chí Kiến trúc số 02-2025)

---

Chú thích
Nghiên cứu này được tài trợ bởi trường Đại học Xây dựng Hà Nội (HUCE) trong đề tài “Nghiên cứu cấu trúc hình học trong tạo hình kiến trúc”, mã số 05-2024/KHXD.

Tài liệu tham khảo
1. Đặng Thái Hoàng (2016): “Phương pháp sáng tác kiến trúc”, NXB Xây dựng, Hà Nội
2. Francis, C. (2012), Architecture: “Form, Space, and Orde”r”, John Wiley & Sons, America
3. Nguyễn Đình Thi và các tác giả (2020): “Giáo trình lịch sử kiến trú”c, NXB Xây dựng
4. Tayyebi, S. and Demir, Y. (2019): “ Architectural Composition: A Systematic Method to Define a List of Visual Attributes”, Art and Design Review, no 7, pp 131-144, doi: 10.4236/adr.2019.73012
5. Rob, K. (1988), Architectural compositon, Academy Edition, Great Britain.
6. Seyed, F. T., Yüksel, D. (2019): “Architectural Composition: A Systematic method to define a list of visual attributes”, Art and Design Review, 2019, 7, pp 131-144
7. https://en.wikipedia.org/wiki/Composition_(visual_arts)
8. https://scratchingsydneyssurface.wordpress.com/2013/10/25/25-october-2013-sydney-opera-house/
9. https://repone.net/ups-downs-hyberbolic-structures-hyperbole/
10. Anas Hameed Majeed et al (2021), Free-form geometries in contemporary architecture – dimensional rules of Folded, Blob and Formlessness architecture, IOP Conf. Ser.: Mater. Sci. Eng. 1058 012043
11. https://www.archdaily.com/496202/ad-classics-los-manantiales-felix-candela
12. https://archeyes.com/national-gymnasium-for-tokyo-olympics-kenzo-tange/
13. https://x.com/HarvardLibrary/status/1420746129138851841/photo/1
14. Hoàng Chúng, Hoàng Quý, Hoàng Tụy (2003), Tìm hiểu Fractal một hình học mới lạ, NXB giáo dục
15. Alik, B., Ayyildiz, S. (2016), “Fractals and Fractal Design in Architecture”, Recent, vol 17(3), pp. 282-291
16. Amal, O., Lobna, S., Sherif, E. (2014), “Fractal geometry in architecture: from formative idea to superficial skin design”, Conference: Contemporary Discussions and Design Methodologies in Architecture ARCHDESIGN ’14At: İstanbul, Turkey
17. Antonio, C. F., Jose, F. R. Jr., Robson L F Cordeiro, (2016), “Effective and Unsupervised Fractal-Based Feature Selection for Very Large Datasets: Removing Linear and Non-linear Attribute Correlations”, Conference: 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), DOI:10.1109/ICDMW.2016.0093
18. https://www.treehugger.com/amazing-Fractals-found-in-nature-4868776
19. https://www.arch2o.com/the-endesa-solar-pavilion-iaac/
20. Amal Osama et al (2014), Fractal geometry in architecture: from formative idea to superficial skin design, Contemporary Discussions and Design Methodologies in Architecture ARCHDESIGN ’14At: İstanbul, Turkey
21. Adc Pronk (2021), Flexible Forming for Fluid Architecture, Springer Cham
22. https://www.archdaily.com/448774/heydar-aliyev-center-zaha-hadid-architects
23. https://architizer.com/projects/zlote-tarasy/
24. https://archestudy.com/turning-torso-wonder-with-the-twist/
25. https://www.iaacblog.com/programs/geometry-and-grid-fosters-and-partners-30st-mary-axe/
26. https://www.archdaily.com/1009690/keeng-seafood-restaurant-bambubuild
27. ttps://www.futurly.com